使用Canvas手画不规则多边形，并限制相交线和凹多边形

简介

使用 Canvas 实现的手画不规则多边形功能。通过鼠标在画面上点击的点作为多边形的顶点，连线形成多边形。除了手画之外，还加入了随机生成和回显，检测多边形横穿，凹凸性的检测。注意：两个点如果靠太近会被认为是同一个点而忽略。闭合区域需要点击图形中的第一个点，或者点击“闭合图形”按钮。

两个 Canvas 图层

由于要实现线条跟随鼠标运动功能，而且 Canvas 的图形无法清除单个绘制命令，因此我用 CSS 的绝对定位，在同一个区域叠加了两个 Canvas 对象。一个在下面，表示已经绘制结束的图形，叫做固定 Canvas；一个在上面，每次鼠标移动就重新绘制跟随鼠标移动的线条，叫做临时 Canvas。canvasTemp 即为临时 Canvas。

<template>
  <div
    class="canvas-box"
    :style="{ width: canvasWidth + 'px', height: canvasHeight + 'px' }"
  >
    <canvas
      ref="canvas"
      :width="canvasWidth"
      :height="canvasHeight"
      class="canvas"
    ></canvas>
    <canvas
      ref="canvasTemp"
      class="canvas"
      :width="canvasWidth"
      :height="canvasHeight"
      @mousedown="draw"
    ></canvas>
  </div>
</template>

<style lang="less" scoped>
.canvas-box {
  margin: 5px auto;
  background: #aaa;
  position: relative;
  .canvas {
    position: absolute;
    top: 0;
    left: 0;
    width: 100%;
    height: 100%;
    cursor: crosshair;
  }
}
</style>

绘制过程

绘画过程简要描述为：

在绘画区域点击第 1 个点，随后线条跟随鼠标移动。
随后点击第 2 — 到第 n 个点，每个点即为多边形的顶点。
点击第一个点闭合图形，或者点击自动闭合图形按钮。

固定 Canvas 绘制

临时 Canvas接收点击事件，得到当前点击的坐标点。

如果是第一个点，则清空之前的绘画区域，并且在固定 Canvas 中移动位置到当前点。
否则检查符合要求后，在固定 Canvas 中绘制一条上一个点到当前点的线。如果符合条件，则闭合图形。
让线跟随鼠标移动。

draw(e) {
  // 点一个当前点
  let pointDown = {
    x: e.offsetX,
    y: e.offsetY,
  };
  // 第一个点
  if (this.pointList.length === 0 || this.closeStatus) {
    this.clear();
    this.canvasObj.beginPath();
    this.canvasObj.moveTo(pointDown.x, pointDown.y);
  } else {
    // 首先检查生成的点是否符合要求
    const check = this.checkPoint(pointDown, this.pointList);
    switch (check) {
      case "closeFirst":
        this.closeFigure();
        return;
      case false:
        return;
      case true:
        break;
    }
    // 已经有点了，连成线
    this.canvasObj.lineTo(pointDown.x, pointDown.y);
    this.canvasObj.stroke();
  }
  this.pointList.push({
    ...pointDown,
  });
  // 如果已经到达最大数量，则直接闭合图形
  if (this.pointList.length >= this.maxPointNum) {
    this.closeFigure();
    return;
  }
  // 让线跟随鼠标移动 后面一节描述
}

临时 Canvas 跟随鼠标移动

在鼠标松开后，监听鼠标移动。在每次鼠标移动的时候，清空临时 Canvas。重新绘制一条点击的坐标点到当前鼠标位置的线。
由于鼠标位置移动很频繁，因此加入了简单的防抖：在下一次dom更新数据后，仅绘制鼠标最后移动到的位置。

// 让线跟随鼠标移动
document.onmouseup = () => {
  document.onmousemove = (event) => {
    // 防抖
    if (this.timeout) {
      clearTimeout(this.timeout);
    }
    this.timeout = setTimeout(() => {
      this.canvasTempObj.clearRect(
        0,
        0,
        this.canvasWidth,
        this.canvasHeight
      );
      this.canvasTempObj.beginPath();
      this.canvasTempObj.moveTo(e.offsetX, e.offsetY);
      this.canvasTempObj.lineTo(event.offsetX, event.offsetY);
      this.canvasTempObj.stroke();
      this.timeout = null;
    });
  };
};

初始化和绘制结束

初始化放在mounted中，主要是设置canvas对象。绘制结束则在检查图形符合要求后，直接闭合图形。检查是否符合要求的方法在后面描述。

// 初始化
mounted() {
  this.canvasObj = this.$refs.canvas.getContext("2d");
  this.canvasObj.lineWidth = 2;
  this.canvasObj.strokeStyle = "red";
  this.canvasObj.fillStyle = "rgba(128, 100, 162, 0.5)";
  this.canvasTempObj = this.$refs.canvasTemp.getContext("2d");
  this.canvasTempObj.lineWidth = 2;
  this.canvasTempObj.strokeStyle = "red";
},

// 闭合图形
closeFigure() {
  // 检查部分
  if (!this.checkPointCross(this.pointList[0], this.pointList)) {
    this.$message.error("闭合图形时发生横穿线，请重新绘制！");
    this.clear();
    return;
  }
  if (!this.checkPointConcave(this.pointList[0], this.pointList, true)) {
    this.$message.error("闭合图形时出现凹多边形，请重新绘制！");
    this.clear();
    return;
  }
  if (this.pointList.length >= this.minPointNum && !this.closeStatus) {
    // 符合要求
    this.canvasTempObj.lineTo(this.pointList[0].x, this.pointList[0].y);
    this.canvasObj.closePath();
    this.canvasObj.stroke();
    this.canvasObj.fill();
    document.onmousemove = document.onmouseup = null;
    this.canvasTempObj.clearRect(0, 0, this.canvasWidth, this.canvasHeight);
    this.closeStatus = true;
    // 绘制结束，返回数据
    this.$emit("drawFinished", this.pointList);
  }
},

// 清除图形
clear() {
  this.pointList = [];
  document.onmousemove = document.onmouseup = null;
  this.canvasTempObj.clearRect(0, 0, this.canvasWidth, this.canvasHeight);
  this.canvasObj.clearRect(0, 0, this.canvasWidth, this.canvasHeight);
  this.closeStatus = false;
},

随机生成和回显图形

随机生成两个整数点作为xy坐标形成多边形顶点，判断是否符合要求，符合要求的顶点列表作为多边形。如果符合要求，则调用回显函数。

随机生成图形

可以看到随机生成的图形中有while (1)循环，还有if (j > num * 100) 这种限制。这是因为目前是随机生成点，再判断是否符合要求，在遇到较复杂的图形限制时，随机生成函数很容易陷入死循环，因此加入了循环失败次数限制。

// 辅助函数，获取随机点
getRandomPoint() {
  const x = Math.floor(Math.random() * this.canvasWidth + 1);
  const y = Math.floor(Math.random() * this.canvasHeight + 1);
  return {
    x,
    y,
  };
},

// 随机生成点并绘制图形
randomRegion() {
  while (1) {
    const num = this.regionNum.min;
    const pointList = [this.getRandomPoint()];
    let i = 1;
    let j = 0;
    while (i < num) {
      const point = this.getRandomPoint();
      // 判断生成的点是否符合要求
      if (this.$refs.canvasRegion.checkPoint(point, pointList) !== true) {
        ++j;
        continue;
      }
      if (j > num * 100) break;
      ++i;
      pointList.push(point);
    }
    // 判断生成的图形是否符合要求
    if (
      pointList.length < num ||
      !this.$refs.canvasRegion.checkPointCross(pointList[0], pointList) ||
      !this.$refs.canvasRegion.checkPointConcave(pointList[0], pointList, true)
    ) {
      continue;
    } else {
      this.$refs.canvasRegion.handleForeignData(pointList);
      break;
    }
  }
},

回显图形

直接在固定 Canvas中绘制即可。

// 处理外来的数据
handleForeignData(canvasData) {
  this.clear();
  if (
    !canvasData ||
    canvasData.length < this.minPointNum ||
    canvasData.length > this.maxPointNum
  ) {
    this.$message.error("回显数据不符合要求！");
    return;
  }
  this.pointList = canvasData;
  this.echoFigure();
},

// 回显图形
echoFigure() {
  this.canvasObj.beginPath();
  this.canvasObj.moveTo(this.pointList[0].x, this.pointList[0].y);
  for (let i = 1; i < this.pointList.length; ++i) {
    this.canvasObj.lineTo(this.pointList[i].x, this.pointList[i].y);
  }
  this.canvasObj.stroke();
  this.closeFigure();
},

点位置的限制

为了防止用户手抖，在同一个位置多次点击鼠标而产生很多顶点，我们增加了点的位置限制。方法很简单：

点击鼠标时，对图形中已有的每个顶点进行循环，每个点判断与鼠标当前位置的距离。如果距离小于要求，则不能生成顶点。
如果与图形中的第一个顶点（就是起点）位置小于要求，则认为用户在尝试闭合图形。

// 检查点有没有与当前点位置太近，如果太近就不认为是一个点
checkPointClose(point, pointList) {
  let i;
  for (i = 0; i < pointList.length; ++i) {
    const distance = Math.sqrt(
      Math.abs(pointList[i].x - point.x) +
        Math.abs(pointList[i].y - point.y)
    );
    if (distance > 3) {
      continue;
    }
    // 如果是在第一个点附近点的，那就认为是在尝试闭合图形
    if (pointList.length >= this.minPointNum && i === 0) {
      return "closeFirst";
    }
    return false;
  }
  return true;
},

相交线的限制

相交线表示多边形的两条边相交。如果允许相交，就会产生下面这种奇怪的图形：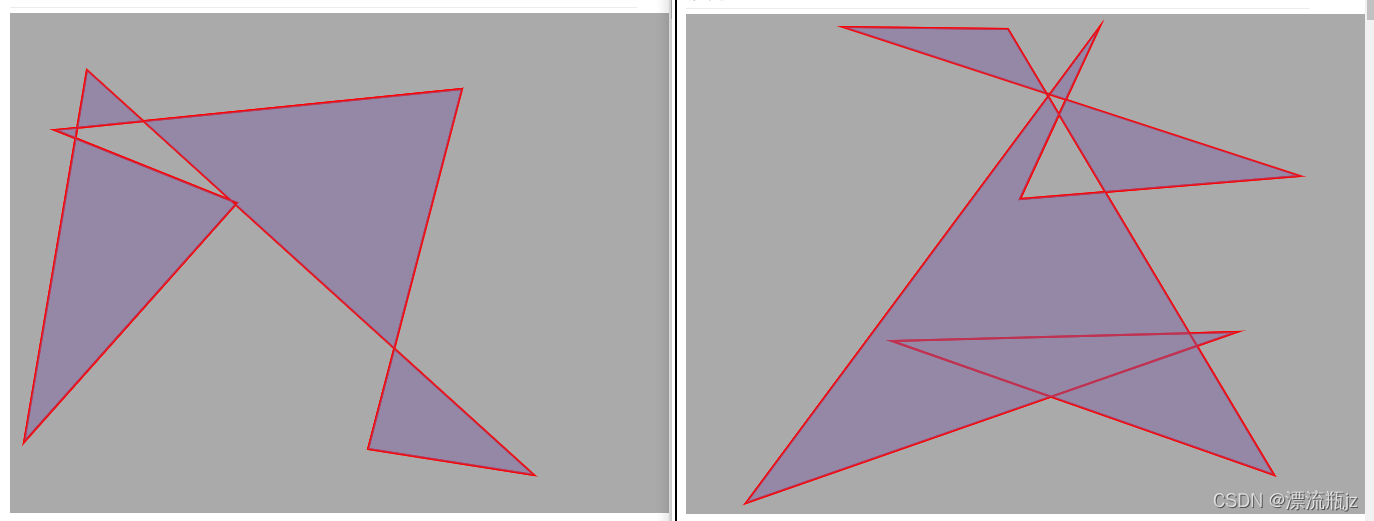

这种图形很明显不像正常的多边形，因此要对相交线进行限制。那么如何判断两条边相交？

小学数学做法

小学数学课的时候，我们都学过如何求两个直线的交点。

\begin{matrix} (x1,y1)&(x2,y2)\quad\overrightarrow{\scriptsize 构造直线方程}\quad y=ax+b\\(x3,y3)&(x4,y4)\quad\overrightarrow{\scriptsize 构造直线方程}\quad y=cx+d\end{matrix}\quad \overrightarrow{\scriptsize 联立求解}\quad(x,y)

最后判断交点（x,y）是否属于两个顶点构成的线段内。
其中，如果a等于c，表示两个直线斜率一致，两个直线平行，无交点。如果同时b等于d，代表两个为同一条直线。最后判断交点是否在线段内非常简单，只需要判断交点的坐标是否在线段两个端点之间即可。
但是，这个方法有个很大的问题：会使用到除法。使用点构造直线方程时会用到除法，联立方程求解交点也会用到除法。计算机中的浮点数是离散存储的，如果是整数可以精确存储。如果使用除法，会产生浮点数，造成精度损失，对于部分边界情况会造成误判。因此不采用这种方法。

向量叉乘判断方向法

向量叉乘

有两个起点在(0,0)，终点在(x1, y1)和(x2, y2)的向量，命名为向量a和b。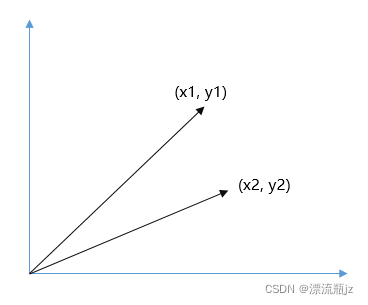两个向量的叉乘定义为：

\begin{vmatrix}x1&x2\\y1&y2\end{vmatrix}=x1*y2-x2*y1

如果叉乘结果为正，则说明向量b在向量a的逆时针方向。如果为正则是顺时针方向。如果为0代表a和b共线。

使用向量叉乘判断交叉

接下来，如果有两条线段分别叫做AB和CD，如何判断两条线是否交叉？

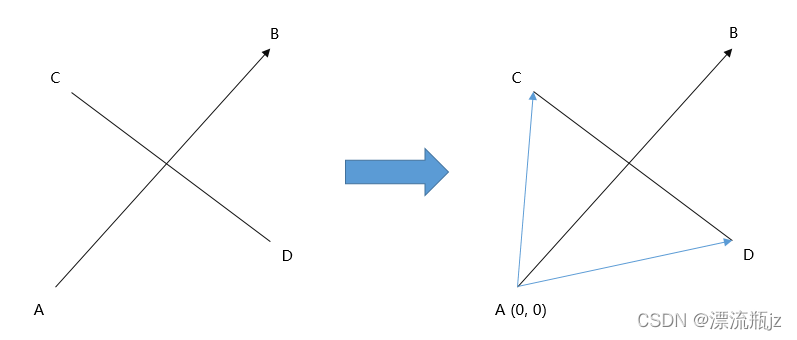
我们令点A作为零点，做AC，AD两条辅助向量。此时我们发现，如果两线交叉，那么C和D必须在直线的两侧。也就是说，向量AB和AC的叉乘与向量AB和AD的叉乘必须是异号的。那么下面这种情况呢？

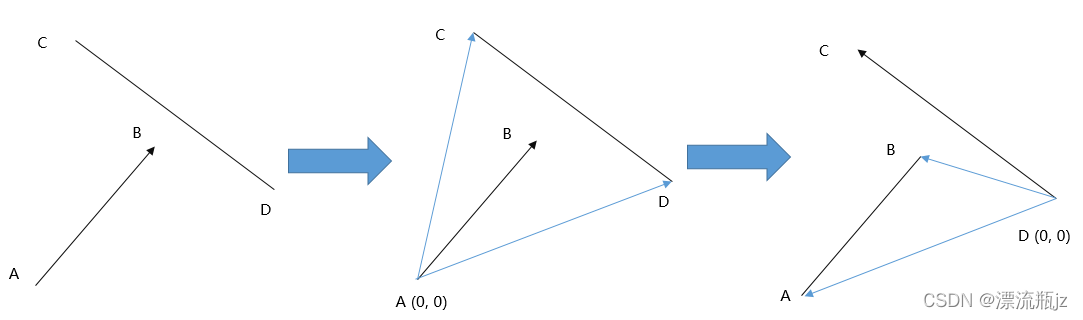
向量AC和AD的确在向量AB的两侧，两条直线交叉，但是线段并不交叉。这时候我们以另一条线段的端点D作为零点，再判断一次发现并不异号。因此，判断两次就能保证交叉。
判断时，我们每点击一个点，就与原来图中的最后一个点连成一条线，再与原来图中所有点判断是否交叉。

// 辅助函数 获取以point1作为原点的线
getPointLine(point1, point2) {
  const p1 = {
    x: point2.x - point1.x,
    y: point2.y - point1.y,
  };
  return p1;
},

// 辅助函数 两线叉乘 两线的起点必须一致
crossLine(point1, point2) {
  return point1.x * point2.y - point2.x * point1.y;
},

// 辅助函数 检查第二条线的方向在第一条线的左还是右
isDirection(point1, point2, point3) {
  // 假设point1是原点
  const p1 = this.getPointLine(point1, point2);
  const p2 = this.getPointLine(point1, point3);
  return this.crossLine(p1, p2);
},

// 辅助函数 判断两个点是否是同一个
isEuqalPoint(point1, point2) {
  if (point1.x == point2.x && point1.y == point2.y) {
    return true;
  }
},

// 辅助函数 检查两个线是否交叉
isPointCross(line1P1, line1P2, line2P1, line2P2) {
  const euqal =
    this.isEuqalPoint(line1P1, line2P1) ||
    this.isEuqalPoint(line1P1, line2P2) ||
    this.isEuqalPoint(line1P2, line2P1) ||
    this.isEuqalPoint(line1P2, line2P2);
  const re1 = this.isDirection(line1P1, line1P2, line2P1);
  const re2 = this.isDirection(line1P1, line1P2, line2P2);
  const re3 = this.isDirection(line2P1, line2P2, line1P1);
  const re4 = this.isDirection(line2P1, line2P2, line1P2);
  const re11 = re1 * re2;
  const re22 = re3 * re4;
  if (re11 < 0 && re22 < 0) return true;
  if (euqal) {
    if (re1 === 0 && re2 === 0 && re3 === 0 && re4 === 0) return true;
  } else {
    if (re11 * re22 === 0) return true;
  }
  return false;
},

  // 检查图形有没有横穿
checkPointCross(point, pointList) {
  if (this.crossAllow) return true;
  let i;
  if (pointList.length < 3) {
    return true;
  }
  for (i = 0; i < pointList.length - 2; ++i) {
    const re = this.isPointCross(
      pointList[i],
      pointList[i + 1],
      pointList[pointList.length - 1],
      point
    );
    if (re) {
      return false;
    }
  }
  return true;
},

如果出现叉乘为0的情况，那么比较复杂，需要首先排除多边形临近边的情况，剩下要分几种情况分别判断。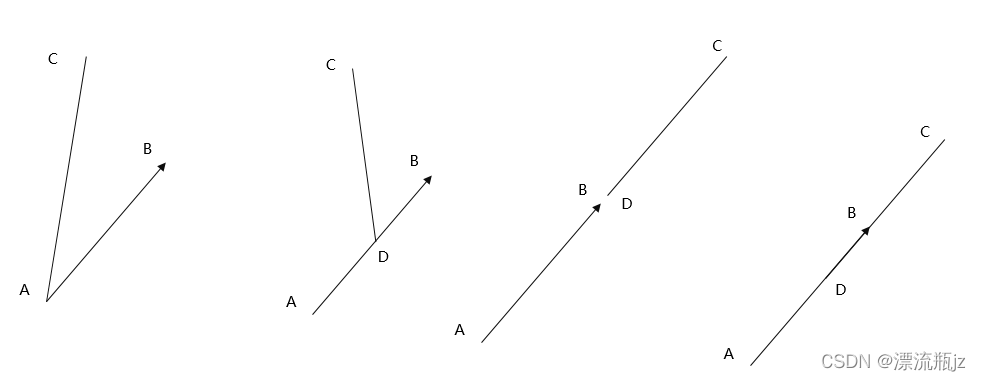

凹多边形限制

凹多边形同样用到上面的叉乘方法来判断。从上面我们知道，向量叉乘可以表示第二个向量在第一个的顺时针还是逆时针方向。我们假设A，B，C是先后画在图中的三个点。我们设A点为零点。连接AC。这时候AB和AC的叉乘>0，表示逆时针。

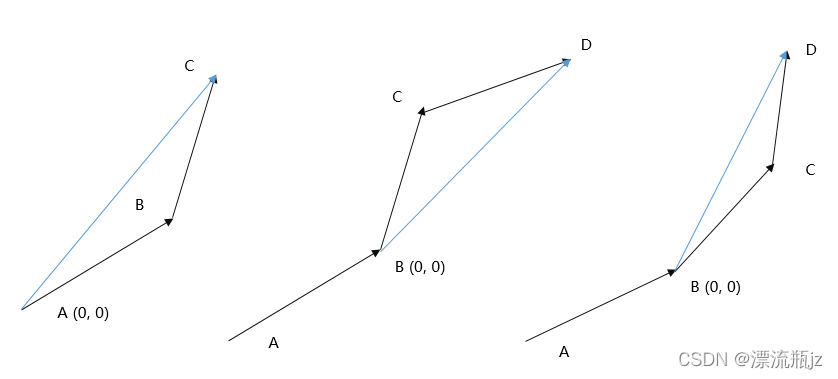
然后我们在图中再画点D。再令点B为零点，连接BD。如果叉乘<0，表示顺时针。这时候我们在图中就会很明显的发现，图形出现凹处。如果叉乘>0，表示逆时针，这时候是可以保证凸多边形的。因此凸多边形的条件是，如果顺序连接图形，每条线的顺逆时针必须一致。

当然也有一些特殊情况，比如图1，虽然每条边都是逆时针符合规则，但是实际上在内卷，如果不交叉线，根本无法闭合。图2很显然是凹多边形，但是凹凸性不一致的边中间的直线上点了好多点，这样就无法通过临近边的叉乘来判断之前线的顺逆时针了。我的解决方法：禁止画这种线，既临近边的叉乘不能为0。还可以有好几个方法能更好的解决：1.顺序记录下每个边的旋转方向，每条边的旋转方向必须一致。 2.可以让图形中任意一个端点连接当前图中的最后一个点，再与当前画的三个点比较凹凸性，如果发现不一致则不是凸多边形。

// 辅助函数 检查三个线是否凹凸
isPointConcave(point1, point2, point3, point4) {
  const re1 = this.isDirection(point1, point2, point3);
  const re2 = this.isDirection(point2, point3, point4);
  if (re1 * re2 <= 0) return true;
  return false;
},

// 检查是否是凹图形
checkPointConcave(point, pointList, isEnd) {
  if (this.concaveAllow) return true;
  let i;
  if (pointList.length < 3) {
    return true;
  }
  if (
    this.isPointConcave(
      pointList[pointList.length - 3],
      pointList[pointList.length - 2],
      pointList[pointList.length - 1],
      point
    )
  )
    return false;

  // 如果是闭合时，point为起始点，需要再判断最后两条线与第一条线是否形成凹图形
  if (isEnd) {
    if (
      this.isPointConcave(
        pointList[pointList.length - 2],
        pointList[pointList.length - 1],
        pointList[0],
        pointList[1]
      )
    )
      return false;
    if (
      this.isPointConcave(
        pointList[pointList.length - 1],
        pointList[0],
        pointList[1],
        pointList[2]
      )
    )
      return false;
  }
  return true;
},

如果是最后闭合图形，则需要判断闭合点附近多条线的顺逆时针。

参考

判断两条线段是否相交—（向量叉乘）
https://www.cnblogs.com/tuyang1129/p/9390376.html
线段的叉乘
https://blog.csdn.net/m0_50089378/article/details/122288557
凸多边形判断 LeetCode 469. 凸多边形
https://blog.csdn.net/weixin_39913117/article/details/111372353

使用Canvas手画不规则多边形，并限制相交线和凹多边形 ​

简介 ​

两个 Canvas 图层 ​

绘制过程 ​

固定 Canvas 绘制 ​

临时 Canvas 跟随鼠标移动 ​

初始化和绘制结束 ​

随机生成和回显图形 ​

随机生成图形 ​

回显图形 ​

点位置的限制 ​

相交线的限制 ​

小学数学做法 ​

向量叉乘判断方向法 ​

向量叉乘 ​

使用向量叉乘判断交叉 ​

凹多边形限制 ​

参考 ​